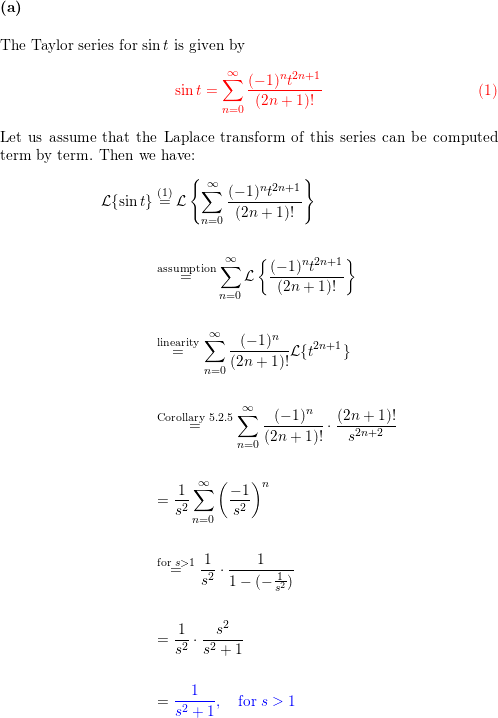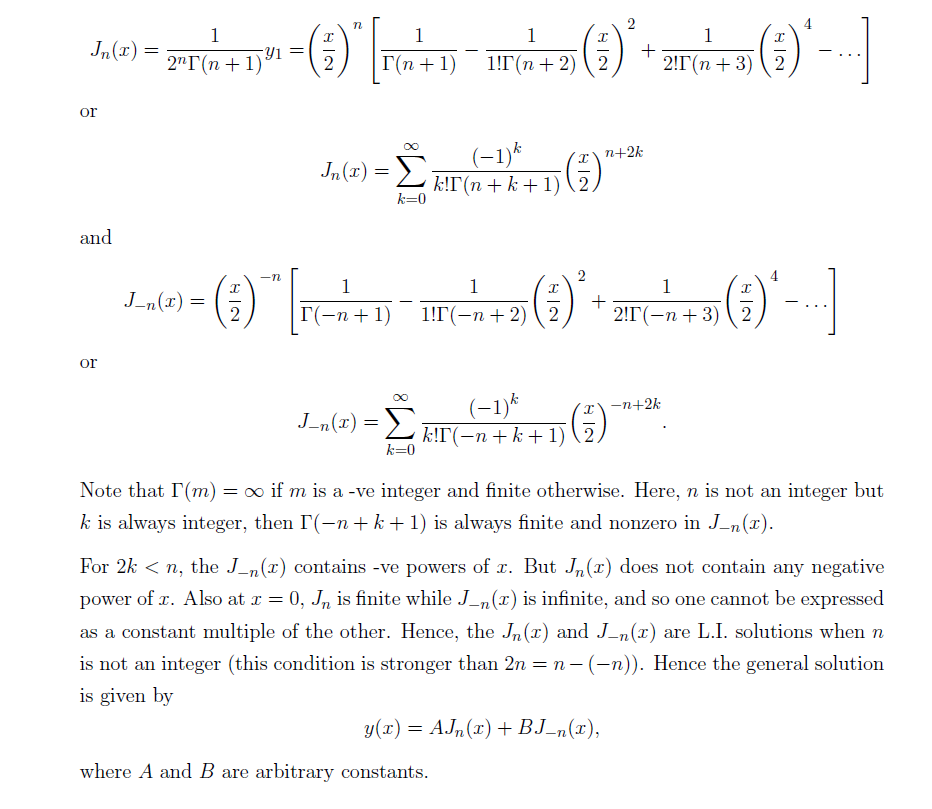Solving Bessel's equation by Laplace transform - Mathematics Stack Exchange
Solved Consider Bessel's equation of order 0 +2 dx2 day + xy | Chegg.com
Bessel function - Wikipedia
Solved We can often use the ODE defining a special function | Chegg.com
SOLVED:We can often use the ODE defining a special function to find its Laplace Transform: Find the Laplace Transform of the Bessel Function of the first kind Jo(x) HINT: Start with a
Limits that contain gamma functions and (products of two) parabolic... | Download Table
ordinary differential equations - Prove that $\int_0^\infty J_0(ax) e^{-px}dx=\frac{1}{\sqrt {a^2+p^2}}$ - Mathematics Stack Exchange
The Bessel function of the first kind of order zero | Chegg.com
SciELO - Brasil - Green's function for the lossy wave equation Green's function for the lossy wave equation
Problem 28
14 Laplace transform of Bessel's Function in Hindi | Laplace Transform of elementary function - YouTube
The Inverse Laplace Transform of the Modified Bessel Function Kmn(a1/2mp1/2m) - Ragab - 1962 - Journal of the London Mathematical Society - Wiley Online Library
Laplace Transform of Bessel Function | Bessel Function | Properties of Bessel Function. - YouTube
Solving Bessel's equation by Laplace transform - Mathematics Stack Exchange
The Laplace transforms of certain functions can be found con | Quizlet
Bessel's Function - SOUL OF MATHEMATICS
PDF) Finite Laplace Transform of spherical Bessel Functions | Indus Foundation International Journals UGC Approved - Academia.edu
Bessel function and its laplace transform - YouTube
Ammaths Tutorials - #13 Laplace transform of Bessel's Function in Hindi | Laplace Transform of elementary function | Facebook | By Ammaths Tutorials | Thanks for watching In This video we are
